Vorticità Potenziale

Pensiero sulla Vorticità Potenziale – Come può aiutare il previsionista?

1.1 Introduzione

Un’Innovazione nella Meteorologia: L’Articolo di Hoskins, McIntyre e Robertson
Un articolo di revisione sulle applicazioni dei concetti di Vorticità Potenziale (PV) scritto da Brian Hoskins, Michael McIntyre e Andy Robertson e pubblicato nel Quarterly Journal of the Royal Meteorological Society nell’ottobre del 1985 (Hoskins et al., 1985; da qui in poi denominato HMR) ha stimolato un significativo aumento del loro utilizzo per comprendere i processi dinamici in meteorologia, principalmente a livello di ricerca.

La Barriera all’Adozione e la Sua Rimozione
Nella mia esperienza, queste idee non sono completamente penetrate fino al livello di previsione quotidiana, principalmente perché, fino a poco tempo fa, i previsionisti non avevano accesso ai grafici PV! Con la recente diffusione di strumenti diagnostici negli uffici di previsione in tutta l’Australia, questo ostacolo è stato superato. Ora, l’unico passo rimasto è convincere i previsionisti che i concetti di vorticità potenziale offrono un valore aggiunto per la comprensione dei fenomeni atmosferici, e vedo questa come una sfida per i ricercatori.

Radici e Riconoscimenti della Vorticità Potenziale
I concetti di vorticità potenziale non sono nuovi: originano dai lavori di Rossby ed Ertel nei primi anni ’40 e sono stati riconosciuti per la loro utilità in una serie di articoli visionari di Kleinschmidt nei primi anni ’50. Una panoramica storica completa è fornita in HMR. I progressi recenti hanno contribuito notevolmente a colmare il divario tra le prime teorie dell’instabilità baroclina di ciclogenesi e le osservazioni effettive. Seguendo i lavori pionieristici di Charney (1947) e Eady (1949), gran parte del lavoro teorico iniziale sull’instabilità baroclina si concentrava sull’evoluzione e la struttura delle piccole perturbazioni in un flusso zonale baroclinico. Al contrario, la ciclogenesi si osserva in concomitanza con disturbi di ampiezza finita all’interno di un flusso zonalmente non uniforme. Tuttavia, la teoria dell’instabilità baroclina predice molte delle caratteristiche osservate nei cicloni reali, come la scala, il tasso di crescita e la struttura delle onde, per esempio, la depressione della pressione che inclina verso ovest con l’altezza.Sebbene la teoria dell’instabilità baroclina possa sembrare una pratica piuttosto esoterica per i previsionisti, un insieme di idee strettamente connesse riguardo alla “guida” e allo “sviluppo” dei cicloni extratropicali, che impiega termini popolari come i “massimi di PVA”, ha guadagnato una posizione di rilievo. Queste nozioni risalgono a un documento del 1947 di Sutcliffe, estremamente acuto e orientato alla pratica, intitolato “La teoria dello sviluppo”. Fondando la sua teoria sulla dinamica quasi-geostrofica, Sutcliffe ha stabilito una base dinamica per alcune regole di previsione fondamentali, come il principio di guida termica. Questo principio sostiene che i cicloni extratropicali tendono a muoversi con la velocità e nella direzione del vento termico tra i 1000 e i 500 mb. Include anche criteri per lo sviluppo e il non sviluppo di cicloni in base alla posizione della bassa pressione superficiale rispetto alla depressione termica, o, in termini equivalenti, a quella a 500 mb. Tuttavia, nonostante Sutcliffe abbia fornito regole pratiche con una solida base dinamica utilizzabili direttamente sul campo, la sua teoria presenta delle limitazioni. Spesso i previsionisti tendono a estenderne l’applicabilità, utilizzandola per costruire argomentazioni o giustificare scenari in cui la teoria non è realmente applicabile. Un errore comune è credere che la teoria sia predittiva, mentre in realtà serve solo a diagnosticare le tendenze in un momento specifico. Inoltre, la teoria è spesso impiegata per formulare ragionamenti di causa ed effetto, quando in realtà riflette solo un aspetto della dinamica della ciclogenesi, considerando soltanto le tendenze iniziali del minimo di superficie come direzione, velocità, approfondimento e riempimento, ma trascurando l’evoluzione reciproca dell’intero sistema, inclusi minimo di superficie e depressione/cresta termica. Una discussione più completa sulla teoria dello sviluppo di Sutcliffe, sui suoi punti di forza e limitazioni, è disponibile nel Capitolo 10 delle mie Note di Lezione sulla Meteorologia Dinamica (Smith, 1998).

Nonostante i limiti, i modelli numerici baroclinici a due strati, pur essendo basilari, hanno dimostrato una maggiore affidabilità rispetto alla teoria di Sutcliffe, data la sofisticatezza e l’affidabilità dei prodotti numerici attuali. Di conseguenza, sarebbe necessario un motivo molto forte per spingere un previsionista a scegliere le regole di Sutcliffe piuttosto che affidarsi ai modelli numerici. Tuttavia, come affermano Davis ed Emanuel (1991), una corretta integrazione delle equazioni del moto non equivale necessariamente a una comprensione concettuale dei fenomeni previsti. Il previsionista desidera non solo disporre di prognosi numeriche, ma anche di un quadro concettuale moderno per interpretarle. È in questo contesto che il “pensiero PV” può essere di aiuto, e il mio ambizioso obiettivo in questo articolo è dimostrare come.

1.2 Cos’è il Pensiero PV?

Esistono due principali metodologie per affrontare i problemi relativi al flusso dei fluidi:

1. La prima implica l’integrazione diretta delle equazioni del momento, della continuità e della termodinamica, note come equazioni primitive.
2. La seconda, applicabile in determinati casi, si basa sull’utilizzo della formulazione vorticità-funzione di corrente.

Il primo metodo, sebbene complesso, può talvolta offrire meno intuizioni dirette sulla dinamica di un fenomeno specifico, parte di questo limite deriva dall’impossibilità di specificare arbitrariamente il campo di forza, come il gradiente di pressione, in un fluido. Questo concetto è approfondito nel mio articolo “Comprendere il moto dei fluidi” (Smith 2003). In contrasto, il metodo vorticità-funzione di corrente fornisce un quadro concettuale più chiaro e diretto per comprendere la dinamica del movimento dei fluidi.

Nella prossima sezione, fornirò alcuni esempi semplici per illustrare meglio questa metodologia. Prima però, desidero spiegare come questa formulazione sia applicata a sistemi di flusso di complessità crescente. In particolare, nel caso di un flusso bidimensionale e non rotante con densità uniforme, questo approccio permette una comprensione più profonda. Qui, la vorticità del fluido, che è un concetto chiave per descrivere il movimento rotatorio, è conservata seguendo le particelle del fluido stesso nel corso del tempo. L’equazione della continuità, poi, suggerisce che esista una funzione di corrente che descrive adeguatamente le componenti della velocità in ogni punto del flusso.Il secondo approccio si occupa di un tipo di equazione differenziale parziale conosciuta come equazione di Poisson, che può essere risolta per ottenere informazioni istantanee riguardo alla distribuzione della vorticità in un fluido, considerando condizioni al contorno appropriate per il dominio di flusso. Questo metodo utilizza la distribuzione di vorticità per aggiornare il campo di vorticità e per diagnosticare i modelli di flusso corrispondenti. In letteratura, queste relazioni sono spesso descritte come relazioni di “invertibilità”, che permettono di trasformare la conoscenza della vorticità in una comprensione del flusso stesso.

Nel caso di un fluido che ruota su un piano specifico, la conservazione della vorticità assoluta è un concetto chiave. Questa conservazione della vorticità include sia la vorticità del fluido che una componente aggiuntiva dovuta alla rotazione del piano. Anche in questo scenario, il concetto di invertibilità rimane valido e sarà dimostrato attraverso esempi pratici nella prossima sezione.

Per flussi che variano in profondità, come quelli con una profondità che cambia nel tempo e nello spazio, si considera la conservazione di un tipo di vorticità che tiene conto sia della vorticità del fluido sia della profondità variabile. In queste condizioni, l’approccio tradizionale per collegare il campo di flusso alla distribuzione di vorticità non è diretto e richiede l’assunzione di un certo equilibrio. Ad esempio, assumendo che il moto del fluido segua approssimativamente un modello quasi-geostrofico, si può semplificare ulteriormente l’analisi di come il flusso e la vorticità sono interconnessi. Questo tipo di analisi aiuta a fornire una comprensione più profonda delle dinamiche di flusso in scenari complessi.Per il moto tridimensionale, quasi-geostrofico di un fluido stratificato rotante, si utilizza un approccio prognostico centrato sulla vorticità potenziale quasi-geostrofica, o pseudo-vorticità potenziale. Questo concetto è basato sulla preservazione di questa vorticità nel tempo, considerando la struttura stratificata e la rotazione del fluido.

In questo contesto, è rilevante una frequenza specifica, nota come frequenza di Brunt-Väisälä, che per semplicità si assume costante. Il metodo di analisi si basa su un’equazione differenziale che relaziona direttamente il potenziale di flusso con la vorticità, garantendo che le condizioni al confine siano appropriate.

Per quanto riguarda il moto adiabatico generale di un fluido stratificato rotante, si conserva una quantità chiamata vorticità potenziale di Ertel. Questa vorticità è influenzata dalla densità del fluido e dalla sua vorticità vettoriale, che comprende il movimento rotatorio del fluido stesso. Particolarmente nelle coordinate isentropiche, questa vorticità assume una forma semplificata che non richiede la considerazione del prodotto scalare e in cui l’avvezione verticale è essenzialmente nulla.

La conservazione di questa vorticità su superfici isentropiche si rivela un risultato molto utile, specialmente quando si analizzano le carte isentropiche di vorticità potenziale per l’atmosfera.

Tuttavia, proprio come nel caso di flussi omogenei divergenti con profondità variabile, non esiste una correlazione univoca tra il campo di flusso e la distribuzione di vorticità potenziale di Ertel a meno che non venga assunto un certo tipo di equilibrio, come l’equilibrio geostrofico o il bilanciamento del vento gradiente. Nonostante queste complicazioni, tali limitazioni non impediscono di costruire argomentazioni valide per flussi atmosferici realistici basati sulla struttura e l’evoluzione della vorticità potenziale di Ertel, similmente a quanto si discuterà con esempi più semplici.

1.3 Esempi di ‘PV-thinking’

Per rispondere alla domanda posta nella sezione precedente, applicherò il ‘PV-thinking’ a tre flussi bidimensionali semplici.

1.3.1 Un esperimento mentale per comprendere il movimento dei cicloni tropicali

Il problema più semplice nella teoria del movimento dei cicloni tropicali considera la traslazione di un vortice inizialmente simmetrico su un piano β a riposo. Gli esperimenti numerici hanno mostrato che un vortice nell’emisfero sud si muove successivamente verso sud-ovest, mentre in quello nord verso nord-ovest. Si presume che il movimento sia uniforme e non varii in intensità, mantenendo così costante la somma di certi parametri vorticosi.

Con il passare del tempo, le particelle d’aria sul lato est del vortice si spostano verso i poli, mantenendo costante la loro caratteristica vorticosa iniziale. Poiché questa caratteristica diventa sempre più marcata verso il ciclone, si verifica un incremento nella tendenza opposta. Al contrario, sul lato ovest del vortice si osserva una tendenza ciclonica crescente nella vorticità relativa. Questo comporta lo sviluppo di una asimmetria nel campo della vorticità che, a causa del movimento del vortice stesso, non rimane fissa ma ruota progressivamente.

Questo movimento non può essere auto-indotto dal vortice simmetrico, ma è piuttosto il risultato del campo di flusso che emerge dall’asimmetria nella vorticità, il quale introduce una componente di movimento verso sud-ovest o nord-ovest, a seconda dell’emisfero considerato.

Per approfondimenti su questo tema e per soluzioni analitiche relative alla distribuzione asimmetrica della vorticità e alle sue implicazioni sul campo di flusso, si possono consultare lavori recenti nel campo. In queste analisi, si illustra come, partendo da una distribuzione di vorticità non uniforme, si possa dedurre il comportamento del flusso circostante, confermando le osservazioni con esempi pratici visualizzati nelle figure.Ora, vorrei mostrare come generalmente utilizziamo la nostra intuizione. Immaginiamo una membrana flessibile con proprietà uniformi tesa su una cornice di filo metallico e sottoposta a una distribuzione costante di forza, come illustrato in una delle figure del testo. Ho descritto il caso in cui la cornice di filo ha la forma di un rettangolo e si trova su un piano orizzontale. Si scopre che la configurazione di equilibrio dello spostamento della membrana rispetta certe regole fisiche e condizioni sui bordi del dominio, ovvero lungo la cornice di filo.

Utilizzando la nostra intuizione, possiamo dedurre qualitativamente come si comporta lo spostamento della membrana; ad esempio, se la forza applicata è positiva in una certa regione, anche lo spostamento della membrana sarà in quella direzione. Questo problema offre un’utile analogia per dedurre la struttura delle soluzioni a un’altra questione fisica, interpretando un parametro come l’opposto della forza sulla membrana e un altro come lo spostamento della membrana stessa. Di conseguenza, le aree con certe caratteristiche nel campo di vorticità tendono ad essere associate a zone opposte in termini di comportamento del flusso.

Tuttavia, dato che la questione riguarda un problema globale, dove la membrana è sotto tensione, i punti estremi nel campo di vorticità non coincidono necessariamente con quelli nel modello di comportamento del flusso, come si può notare confrontando due diverse figure illustrate nel testo. Una piccola modifica nel modo di affrontare il problema della membrana ci permette inoltre di applicare diversi tipi di condizioni al bordo, come dettagliato in una sezione specifica di un lavoro di riferimento.

La Figura 1.1 illustra un esperimento teorico semplice per comprendere il movimento dei cicloni tropicali nell’emisfero sud, utilizzando un piano β. Ecco una spiegazione dettagliata delle diverse parti della figura:

• Panello (a): Questo diagramma mostra un vortice simmetrico che si muove in un ambiente senza flussi di base esterni. La linea tratteggiate indica la traiettoria del vortice verso sud-ovest. Il vortice ruota in senso antiorario, come evidenziato dalla freccia circolare.
• Panello (b): Presenta l’evoluzione dell’asimmetria della vorticità (ζa) dopo 24 ore. Questa asimmetria si manifesta come un modello a spirale o anello, con le linee tratteggiate che rappresentano i valori negativi della vorticità. Questo mostra le modifiche nella velocità di rotazione del vortice a causa di influenze esterne.
• Panello (c): Illustra il modello asimmetrico della funzione di corrente (ψa), che corrisponde all’asimmetria della vorticità ζa. Questo modello è stato derivato analiticamente e mostra i contorni del flusso, con le linee continue per i valori positivi e le linee tratteggiate per quelli negativi. Questi contorni offrono una visione su come il flusso si muove in risposta alla distribuzione modificata della vorticità.

In conclusione, la Figura 1.1 aiuta a visualizzare come un vortice inizialmente uniforme possa sviluppare asimmetrie nel campo di vorticità e di flusso a causa delle variazioni locali della forza di Coriolis (effetto β) e come queste asimmetrie influenzino la traiettoria del vortice. Questo è essenziale per capire la dinamica dei cicloni tropicali e le loro traiettorie previste.

1.3.2 Instabilità di taglio Kelvin-Helmholtz

Molti casi di turbolenza in aria limpida sono ritenuti associati a una forma di instabilità di taglio, che si verifica quando il taglio del vento verticale in uno strato d’aria stratificato stabilmente è notevole. Un modello idealizzato per questa instabilità considera due flussi d’aria paralleli e omogenei con velocità costanti U1 e U2. In questo modello, il taglio è concentrato all’interfaccia tra i flussi, rappresentata come un foglio sottile di vorticità orizzontale.

L’instabilità di questo flusso può essere compresa attraverso l’analisi della vorticità. Immaginiamo che il foglio di vortice sia perturbato da una distorsione ondulatoria sinusoidale. L’evoluzione successiva del campo di vorticità è guidata dalle leggi della fisica che considerano le dimensioni orizzontale x e verticale y. Un particolare interesse è posto sul comportamento di una particella materiale al punto B, dove lo spostamento verticale è massimo. Qui, il movimento è influenzato dalla distribuzione di vorticità in tutti gli altri punti, con elementi vortice nei punti A e C che inducono contributi di velocità, risultando in una componente orizzontale netta verso C.

Inizialmente, quindi, la vorticità nel foglio tende a raggrupparsi in regioni tra B e D, portando alla formazione di centri isolati di vorticità. Questo processo può rompere la simmetria iniziale della distribuzione di vorticità, inducendo una velocità che aumenta lo spostamento laterale dei punti B e D. Questo può diventare un processo auto-alimentato, a meno che non venga controllato da non linearità man mano che l’ampiezza dello spostamento cresce. Questo esempio dimostra l’applicazione del principio di invertibilità senza riferimento diretto alla soluzione specifica, ma i concetti sono comunque intercambiabili.

La Figura 1.2 illustra lo spostamento di equilibrio ξ(x, y) di una membrana tesa su una cornice quadrata, influenzata da una distribuzione di forza F(x, y). La griglia nella figura rappresenta la membrana, che mostra come si deforma in risposta alle forze applicate.

• Nei punti dove la forza F < 0, osserviamo che la membrana viene spinta verso il basso, indicando una depressione causata dalla forza negativa.
• Dove la forza F = 0, la membrana non mostra deformazioni significative e rimane al livello della cornice.

Questa rappresentazione visiva aiuta a intuire come la membrana reagisce alle variazioni delle forze esterne. Il modello suggerisce che la deformazione della membrana segue le soluzioni dell’equazione di Poisson, che descrive matematicamente il profilo di deformazione in risposta alle forze.

Le linee di contorno mostrate nella griglia aiutano a visualizzare l’intensità e la direzione dello spostamento in ogni punto della membrana. Questa visualizzazione è cruciale per comprendere e prevedere il comportamento di materiali elastici sottoposti a carichi in diverse applicazioni, sia ingegneristiche che fisiche.

La Figura 1.3 illustra il fenomeno dell’instabilità di taglio di Kelvin-Helmholtz, evidenziando l’amplificazione autoindotta di un foglio di vortice distorto.

1. Due Correnti d’Aria: La figura presenta due correnti d’aria parallele che fluiscono con velocità uniformi, U1 e U2. La corrente U1 scorre sopra U2, creando una configurazione tipica per l’instabilità di Kelvin-Helmholtz dove la differenza di velocità tra i due strati di fluido può portare a instabilità.
2. Distorsione del Foglio di Vortice: Inizialmente piatto, il foglio di vortice viene distorto da perturbazioni, formando un’onda con punti di cresta (A e C) e punti di avvallamento (B e D).
3. Movimento Indotto:
   • Nei punti A e C, la velocità indotta tende a spostare il fluido verso l’alto.
   • Al punto B, si verifica lo spostamento massimo verso l’alto.
   • Al punto D, la velocità indotta spinge verso il basso, intensificando l’avvallamento.
4. Effetto di Amplificazione:
   • La parte inferiore della figura mostra come le iniziali perturbazioni del foglio di vortice conducano a movimenti estremi nelle creste e negli avvallamenti, amplificando ulteriormente la distorsione.
   • Questo meccanismo di feedback positivo è autoindotto: la distorsione del foglio di vortice genera velocità che, a loro volta, intensificano ulteriormente la distorsione, promuovendo un’instabilità crescente.

Questa rappresentazione aiuta a comprendere come le piccole perturbazioni iniziali in un sistema con forti gradienti di velocità possano evolvere in grandi distorsioni tramite meccanismi di feedback positivo, un principio fondamentale per interpretare vari fenomeni in atmosfera e oceani.

La Figura 1.4 mostra un esempio delle onde di Rossby, che sono onde di scala planetaria importanti nelle dinamiche atmosferiche e oceaniche. Queste onde si formano a causa delle variazioni della forza di Coriolis con la latitudine e sono essenziali per comprendere i modelli di circolazione globale.

1. Contorni di Vorticità Assoluta (linee solide): Le linee solide rappresentano i contorni di vorticità assoluta (ζ + f = costante), con ζ che rappresenta la vorticità relativa e f la vorticità planetaria. Questi contorni seguono un modello sinusoidale lungo una banda di latitudini in un canale del piano β.
2. Campo di Velocità Indotto: Le frecce indicano il campo di velocità indotto dalle variazioni di vorticità. Questo campo di velocità si alterna, rispondendo ai cambiamenti nella vorticità, e facilita il trasferimento di energia e momento attraverso l’atmosfera o l’oceano.
3. Dinamica delle Onde: Le onde di Rossby caratterizzano movimenti del fluido che tentano di riportare il sistema all’equilibrio. Le frecce mostrano questo movimento fluido lungo i contorni di vorticità, enfatizzando la natura ondulatoria delle perturbazioni.
4. Interazione tra Vorticità e Movimento del Fluido: Questa interazione è cruciale per la propagazione delle onde di Rossby, influenzando i modelli climatici e meteorologici su larga scala.

In conclusione, la Figura 1.4 illustra come le onde di Rossby modulano il clima e i pattern meteorologici attraverso la relazione tra vorticità assoluta e il campo di velocità indotto, fornendo una visione chiara delle loro dinamiche nel contesto di un canale del piano β.

Propagazione delle Onde di Rossby su un Canale del Piano β

Il nostro terzo esempio offre un’interpretazione della dinamica delle onde di Rossby, anche note come onde planetarie, in un canale situato a medie latitudini come discusso da McIntyre. Immaginiamo che il canale sia delimitato da confini rigidi a specifiche latitudini. Lo stato di base è considerato uno di quiete relativa, con una variazione uniforme della frequenza di Coriolis da nord verso sud.

Nei contorni della vorticità assoluta dello stato di base, considerati costanti, si trovano lungo i cerchi di latitudine. Se un disturbo causa un’ondulazione sinusoidale di questi contorni, come mostrato nell’illustrazione, l’effetto perturbatore varierà anche esso sinusoidalmente, presentando alternanza di segni positivi e negativi. Per comprendere l’aspetto del campo indotto possiamo paragonarlo a una membrana elastica che viene spinta e tirata in un modello simile. I bordi della membrana sono fissi, senza spostamenti, lungo le linee che corrispondono ai confini del canale.

Secondo questa analogia, il modello del campo sarà simile a quello della perturbazione, ma con segno opposto. Questo comporta che il campo mostrerà elevazioni e depressioni centrate rispettivamente sui punti di segno negativo e positivo, con i venti più forti disposti nord-sud in posizioni intermedie, sfasati di un quarto di lunghezza d’onda rispetto allo spostamento. L’effetto di questo campo di velocità sui contorni è che le ondulazioni si muoveranno verso ovest. I movimenti risultano stabili, o per essere più precisi, neutramente stabili, poiché la perturbazione di velocità è nulla dove gli spostamenti delle particelle dalle loro posizioni di equilibrio sono massimi.

In ogni esempio, il ragionamento segue lo stesso schema. Dapprima si determina la distribuzione di vorticità dovuta alla proprietà di conservazione, quindi si utilizza il principio di invertibilità per dedurre il campo di flusso associato a questa distribuzione, che generalmente è legato ad anomalie nella vorticità.

La Figura 1.5 mostra la distribuzione delle variabili P e q sotto i 100 millibar durante l’inverno nell’emisfero nord. Ecco una descrizione dettagliata degli elementi chiave della figura:

• Contorni tratteggiati: Rappresentano le linee di livello per q, che cambia a intervalli di temperatura atmosferica. Questi contorni aiutano a visualizzare come questo parametro varia con l’altitudine e la latitudine.
• Valori di P: Sono misurati in unità che rappresentano la vorticità potenziale, un concetto chiave nella dinamica atmosferica. I contorni sono disegnati per diversi livelli di questa unità, segnalando variazioni significative della vorticità atmosferica.
• Tropopausa dinamica: Indicata con una zona puntinata, corrisponde a un livello specifico di vorticità potenziale. Questa zona rappresenta il confine tra la troposfera, dove avvengono la maggior parte dei fenomeni meteorologici, e la stratosfera superiore. La definizione di questo limite è fondamentale per studi sul tempo e sul clima.
• Scalatura verticale e orizzontale: L’asse verticale indica la pressione atmosferica in millibar, mostrando come cambia da vicino la superficie terrestre fino a altezze più elevate. L’asse orizzontale mostra le latitudini che vanno dal Polo Nord all’equatore.

Questa rappresentazione aiuta a comprendere come determinati parametri atmosferici si distribuiscono verticalmente e geograficamente, influenzando le condizioni meteorologiche e climatiche dell’emisfero nord durante i mesi invernali.

La struttura dell’EPV nell’atmosfera

Prima di esplorare come le idee discusse in precedenza possano essere applicate all’atmosfera, analizziamo la struttura media dell’EPV nell’atmosfera, oltre alle sue variazioni quotidiane. La Figura 1.5 illustra la distribuzione climatologica di P e la temperatura potenziale θ, mediata zonalmente, per l’inverno dell’emisfero nord. Dalla regione polare fino a circa 25° di latitudine, la superficie con un valore specifico di P coincide con la tropopausa, che rappresenta il limite tra la troposfera e la stratosfera.

I valori di PV nella troposfera sono tipicamente minori di un certo limite e sono strettamente collegati alla variazione della densità dell’aria con l’altitudine. Vi è un aumento marcato alla tropopausa dovuto al cambiamento nella stabilità dell’aria. I valori di PV nella stratosfera sono generalmente molto più alti.

Alle latitudini più vicine all’equatore, inferiore a circa 25°, i valori di PV diminuiscono con l’approssimarsi all’equatore. In questa regione, le superfici di PV tendono ad inclinarsi verso l’alto man mano che si avvicinano all’equatore.

La variazione tipica di PV lungo le superfici isentropiche è evidente anche dalla figura. Ad esempio, lungo una superficie isentropica che si trova principalmente nella troposfera, i gradienti di PV sono generalmente bassi. Al contrario, una superficie che campiona l’aria stratosferica ad alte latitudini e l’aria della troposfera media a basse latitudini mostra gradienti di PV bassi verso l’equatore e alti verso i poli. Una superficie isentropica che campiona principalmente l’aria stratosferica mostra variazioni significative solo nelle latitudini molto basse.

Mappe di Vorticità Potenziale Isentropica

HMR presentano grafici dei contorni di PV nell’emisfero nord su superfici isentropiche scelte per una specifica situazione sinottica, comparando le caratteristiche su queste con quelle di carte più tradizionali. Per esempio, hanno evidenziato che elementi significativi nelle carte isobariche dell’altezza geopotenziale, come fosse, creste, minimi isolati e anticicloni bloccanti, corrispondono a caratteristiche distintive sulle mappe isentropiche di PV. Un estratto dalla loro figura 1.2 è visibile nelle figure 1.6 e 1.7.

Come anticipato in precedenza, i gradienti di PV sono pronunciati in una regione che circonda il polo dove la superficie isentropica si trova nella stratosfera, ma risultano più deboli dove la superficie si estende verso l’equatore nella troposfera. La tropopausa, indicata approssimativamente dalla regione scura nelle figure 1.6 e 1.7b, è marcatamente contorta e vi sono piccole aree dove l’aria con alto PV è completamente circondata da aria a basso PV e viceversa. Questi fenomeni possono essere collegati, rispettivamente, ai minimi isolati e agli anticicloni bloccanti nei campi geopotenziali. In altre zone, lunghe lingue di aria ad alto PV si estendono dal serbatoio stratosferico mentre lingue di aria a basso PV avanzano verso il polo in una regione normalmente occupata dall’aria stratosferica sulla data isentropa. Questi aspetti tendono ad associarsi rispettivamente con le fosse e le creste sulle carte isobariche. Caratteristiche specifiche sono indicate nelle figure 1.6 e 1.7. La caratteristica A è principalmente un elemento di livello superiore e corrisponde a un minimo nella troposfera superiore, mentre B è associata a una depressione di livello superiore.La caratteristica C corrisponde a una depressione che attraversa tutta la profondità della troposfera, mentre la depressione D è prevalentemente un fenomeno di alto livello. HML, nelle figure 1.3 e 1.4, presentano sequenze temporali delle mappe di vorticità potenziale (PV) per illustrare l’evoluzione di diversi sistemi atmosferici e confrontano queste evoluzioni con i cambiamenti nei campi di altezza geopotenziale su superfici isentropiche selezionate. Essi includono anche un esempio della formazione di un minimo isolato, mostrato nella figura 1.8a.

In questo caso specifico, un’anomalia dell’aria superiore, costituita da aria stratosferica con alta vorticità potenziale, è stata trasportata dall’area vicino allo Stretto di Hudson attraverso l’Atlantico verso l’Europa, e sembra che si sia avvolta formando un grande ciclone isolato il 24 settembre a 18° Ovest. La figura 1.8b mostra le altezze geopotenziali a 500 millibar che corrispondono a queste mappe di PV, mentre la figura 1.9 illustra i campi di altezza geopotenziale a 1000 millibar e di temperatura a 700 millibar per il periodo dal 22 al 24 settembre, durante il quale si è verificato il distacco. Questo evento rappresenta un esempio di formazione ciclonica piuttosto semplice, in cui una singola anomalia di vorticità potenziale dell’aria superiore è stata trasportata in una regione in cui, rispetto al suo ambiente originario, risultava meno anomala. Questo ci spinge ad indagare sulla struttura verticale tipica di tali anomalie, con alcune indicazioni fornite dagli studi di Thorpe nei mid-anni ’80.

La Figura 1.6 mostra le mappe di vorticità potenziale (PV) dell’emisfero nord su una superficie isentropica specifica a 350 K, datata 30 settembre 1982. Ecco una descrizione dettagliata dei principali elementi visualizzati nella mappa:

1. Contorni Neri: Alcune regioni della mappa sono evidenziate in nero, segnalando aree con una significativa concentrazione di vorticità potenziale.
2. Vettori di Velocità: Sono rappresentati i vettori che mostrano la direzione e l’intensità del vento su questa superficie. La posizione delle frecce indica il flusso del vento e la loro lunghezza fornisce un’indicazione della velocità del vento, con una scala specifica che suggerisce che una certa lunghezza di freccia corrisponde a una velocità di 100 metri al secondo.
3. Cerchio Esterno: Il cerchio che delimita la mappa rappresenta l’equatore, mostrando il limite geografico della rappresentazione dell’emisfero nord.
4. Lettere: Le lettere indicate nella mappa (A, B, C, D, D’) identificano particolari caratteristiche meteorologiche discusse nel testo di accompagnamento, quali sistemi di bassa pressione o altre formazioni significative nell’atmosfera.

Questa mappa è utilizzata per visualizzare la distribuzione e le caratteristiche della vorticità potenziale su una determinata superficie isentropica, permettendo agli studiosi di mettere in relazione questi dati con la dinamica atmosferica e le condizioni meteorologiche del periodo in questione.

La Figura 1.7 illustra vari campi sinottici per l’emisfero nord al 30 settembre 1982, mostrando una complessa analisi meteorologica attraverso diverse mappe:

1. Mappe di Vorticità Potenziale (PV)
   • (b) Mappa a 330 K: Questa mappa visualizza la distribuzione di vorticità potenziale a questa specifica altezza. Le aree con maggiore vorticità sono marcate in nero, indicando zone di particolare interesse meteorologico.
   • (c) Mappa a 315 K e (d) Mappa a 300 K: Simili alla precedente, ma a differenti altezze, queste mappe evidenziano anche le aree con intensa vorticità, aiutando a comprendere meglio la struttura verticale dell’atmosfera in questi livelli.
2. Vettori del Vento: Come in mappe precedenti, questi indicano la direzione e l’intensità dei venti a queste altitudini, con il confine del cerchio posizionato a 20°N, diversamente dall’equatore.
3. Campi di Altezza Geopotenziale
   • (f) Altezza a 250 mb e (g) Altezza a 1000 mb: Forniscono una rappresentazione delle altezze geopotenziali a queste due diverse pressioni atmosferiche. Sono strumentali per analizzare la disposizione e il movimento delle masse d’aria all’interno dell’atmosfera.
4. Contorni di Pressione
   • (e) Contorni sulla Superficie a 315 K: Mostra come la pressione si distribuisce su questa superficie isentropica, utile per identificare zone di alta e bassa pressione che influenzano i movimenti atmosferici.

Ogni segmento di questa figura contribuisce a una comprensione dettagliata delle condizioni atmosferiche di quel giorno, offrendo informazioni cruciali per l’analisi di eventi meteorologici come cicloni e anticicloni. Questa disposizione di mappe aiuta gli studiosi e meteorologi a visualizzare e interpretare la dinamica dell’atmosfera in modo più efficace.

La Figura 1.8 offre una visione dettagliata di due diversi aspetti meteorologici sopra l’emisfero nord per il periodo tra il 20 e il 25 settembre 1982:

1. (a) Mappe di Vorticità Potenziale (PV) a 300 K:
   • Copertura Geografica: Le mappe coprono l’area dai 40°N fino al Polo Nord e da 120°W a 0°W, centrando il meridiano di 60°W.
   • Intervalli dei Contorni: I contorni sono delineati ogni 0.5 unità di PV. Le aree con valori di PV tra 1.5 e 2 sono marcate in nero, indicando regioni di intensa attività atmosferica.
   • Vettori di Velocità Orizzontale: Vengono visualizzati i vettori di velocità, utilizzando la stessa scala della Figura 1.5, per mostrare direzione e velocità dei venti a questa quota.
2. (b) Altezze Geopotenziali a 500 mb:
   • Intervalli dei Contorni: I contorni sono tracciati ogni 100 metri, corrispondendo alle mappe di PV in (a) per dare un’immagine più chiara della struttura verticale dell’atmosfera nella regione analizzata.

Questi elementi sono fondamentali per i meteorologi per analizzare e seguire l’evoluzione dei sistemi meteorologici, in particolare per capire come le anomalie di vorticità potenziale si correlano con variazioni nelle altezze geopotenziali. Identificare le zone di alta vorticità potenziale può essere cruciale per prevedere la formazione di cicloni e altre instabilità atmosferiche. Le mappe consecutive permettono agli esperti di monitorare dinamiche atmosferiche nel tempo, migliorando la previsione e la comprensione dei fenomeni meteorologici.

La Figura 1.9 illustra due serie di mappe meteorologiche per il periodo dal 22 al 24 settembre 1982, coprendo la regione tra 40°N e 90°N e tra 120°W e 0°W, la stessa area geografica mostrata nella Figura 1.8.

1. (a) Altezze Geopotenziali a 1000 mb:
   • Queste mappe forniscono una rappresentazione delle altezze geopotenziali a 1000 millibar, con contorni tracciati ogni 60 metri. Le altezze geopotenziali sono essenziali per comprendere le strutture di pressione a bassa quota che influenzano direttamente i modelli di circolazione atmosferica e le condizioni meteorologiche al livello del suolo.
2. (b) Temperature a 700 mb:
   • Le mappe visualizzano i contorni delle temperature a 700 millibar, con intervalli di contorno di 5 Kelvin. Questo livello di pressione nella troposfera media è critico per analizzare le condizioni che influenzano la formazione di nuvole, i movimenti dei fronti meteorologici e altre dinamiche atmosferiche.

Insieme, queste mappe offrono una visione comprensiva delle condizioni atmosferiche in termini di pressione e temperatura, cruciali per le previsioni meteorologiche e l’analisi della dinamica atmosferica. Studiando queste mappe, i meteorologi possono identificare aree di alta e bassa pressione, valutare la stabilità atmosferica e tracciare l’evoluzione di importanti sistemi meteorologici.

La struttura verticale delle anomalie di vorticità potenziale dell’aria superiore

La Figura 1.10 illustra la struttura verticale dei disturbi associati alle anomalie asimmetriche di vorticità potenziale nell’aria superiore. Questi diagrammi derivano da soluzioni numeriche del problema di inversione per la EPV (vorticità potenziale equivalente), presupponendo che i disturbi siano in equilibrio con il vento gradiente. Un’anomalia positiva, situata vicino alla tropopausa (Fig. 1.10a), è caratterizzata da una circolazione ciclonica, mentre un’anomalia negativa (Fig. 1.10b) presenta una circolazione anticiclonica. La circolazione è massima al livello dell’anomalia e decresce con l’altezza sopra e sotto di essa. Le isentrope mostrano un modello distintivo: per un’anomalia positiva, sono elevate sotto l’anomalia, segnalando una stabilità statica ridotta, e abbassate sopra, evidenziando una tropopausa più bassa nelle vicinanze dell’anomalia. Per un’anomalia negativa (anticiclonica), queste caratteristiche sono invertite, con una maggiore stabilità statica sotto l’anomalia e una tropopausa elevata sopra di essa. Tali strutture sono piuttosto realistiche; ad esempio, la Figura 1.11 mostra la struttura isentropica analoga attraverso un basso isolato in un’analisi osservativa precoce di Peltonen (1963). In un’anomalia stazionaria, non si verifica alcun moto verticale.

Un aspetto rilevante di queste strutture è che si spostano insieme all’anomalia, se questa si muove. Ciò suggerisce l’esistenza di un modello di movimento verticale. Per esempio, man mano che un’anomalia positiva procede, l’aria sottostante e antistante deve ascendere lungo le isentrope elevate, mentre l’aria posta dietro scende lungo le stesse. Il contrario si verifica per un’anomalia negativa in movimento. Nella realtà, questi modelli di movimento verticale si possono correlare alle aree osservate di nuvolosità o di cieli sereni nei sistemi atmosferici. Nel prossimo capitolo, continueremo ad esplorare altri tipi di eventi di ciclogenesi nell’ambito della vorticità potenziale.

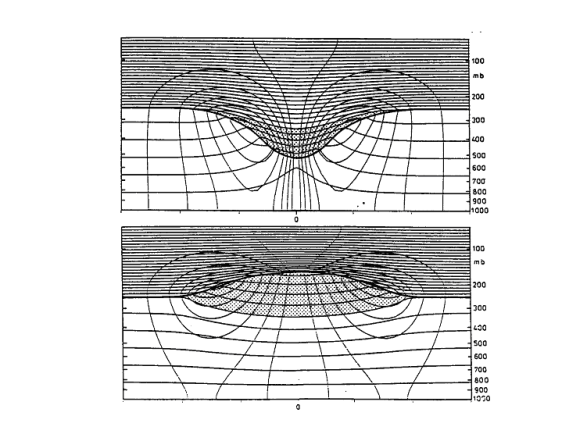
La Figura 1.10 illustra flussi circolarmente simmetrici causati da anomalie isolate di vorticità potenziale (PV) a livelli alti, con le aree di anomalia indicate tramite trame a punti. La figura include due pannelli distinti:

1. Pannello superiore: Mostra il flusso risultante da un’anomalia positiva di PV. Le linee quasi-orizzontali sono le isentrope, che rappresentano superfici di temperatura potenziale costante, utili per analizzare la distribuzione verticale di calore e umidità. Le linee più sottili sono le isotache, che indicano velocità del vento costante. La linea spessa rappresenta la tropopausa, il confine tra la troposfera e la stratosfera. Questa anomalia positiva induce una circolazione ciclonica, che solleva le isentrope sotto l’anomalia e le abbassa sopra di essa, indicando una ridotta stabilità statica sotto e maggior stabilità sopra l’anomalia.
2. Pannello inferiore: Raffigura il flusso causato da un’anomalia negativa di PV. A differenza del pannello superiore, qui l’anomalia negativa porta a una circolazione anticiclonica. Le isentrope sono abbassate sotto l’anomalia, mostrando una maggiore stabilità statica, e sollevate sopra, riflettendo una ridotta stabilità e una tropopausa elevata sopra l’anomalia.

Questi schemi di flusso sono essenziali per comprendere come le anomalie di PV modifichino la struttura atmosferica circostante, influenzando il tempo e il clima attraverso la modulazione della stabilità atmosferica e dei movimenti verticali.

La Figura 1.11 mostra una sezione verticale attraverso un ciclone tagliato alle 12 GCT del 16 novembre 1959, analizzato da Peltonen nel 1963. Questo diagramma offre una visione dettagliata delle strutture termiche e dinamiche all’interno del ciclone. Ecco le componenti principali illustrate nella figura:

1. Linea spessa: Rappresenta la tropopausa, il limite superiore della troposfera, dove si verifica un netto cambiamento nel gradiente di temperatura.
2. Linee tratteggiate: Sono le isoterme, che indicano linee di temperatura costante. Queste linee sono tracciate a intervalli di 50°C e mostrano la distribuzione termica all’interno del ciclone.
3. Linee continue: Rappresentano le isentrope, linee di entropia termica costante, distanziate ogni 5 K. Queste linee aiutano a capire la distribuzione verticale di energia e stabilità all’interno del ciclone.

Il centro del ciclone è posizionato a 350°E, 58°N, indicando una specifica posizione geografica. Analizzare cicloni isolati come questo, che sono separati dalle principali correnti atmosferiche, è essenziale per capire il movimento dell’aria sia verticalmente che orizzontalmente all’interno di un sistema chiuso. Questo influisce sulle condizioni meteorologiche, sul trasporto di energia e umidità, e fornisce insight importanti per la meteorologia sinottica e le previsioni meteorologiche.

Capitolo 2 Una visione della ciclogenesi attraverso la Vorticità Potenziale

2.1 Idee Preliminari Nel capitolo precedente, abbiamo esaminato un tipo basilare di ciclogenesi che conduce alla formazione di un basso isolato. Tuttavia, questo non rappresenta l’unico tipo e non è associato con le conversioni di energia baroclinica. Come si manifestano quindi tali conversioni energetiche in una descrizione basata sulla Vorticità Potenziale (PV)? La soluzione a questo quesito trae origine da un lavoro di Bretherton nel 1966, ed è stata successivamente perfezionata da McIntyre nei primi anni ’70 attraverso appunti di lezione non pubblicati. Bretherton ha dimostrato che i gradienti di temperatura presenti ai confini delle zone barocliniche a basso livello sono matematicamente equivalenti a sottili strati di vorticità potenziale appena sopra il confine, con un gradiente orizzontale proporzionale al gradiente di temperatura. In particolare, le anomalie di temperatura isolate ai confini corrispondono a anomalie di vorticità potenziale del segno appropriato. Questa idea rivoluzionaria permette di presentare una visione unificata del meccanismo di instabilità baroclinica in termini di PV, consentendo altresì un approccio analogo per la ciclogenesi. Data l’importanza di tale risultato, tenterò di illustrare come si arrivi a questa conclusione mediante un semplice calcolo.

2.2 Strati superficiali del PV

Desidero illustrare come un gradiente di temperatura orizzontale sulla superficie possa essere visto come equivalente a uno strato molto sottile di vorticità potenziale (PV) proprio sulla superficie. Questa dimostrazione è valida nel contesto di un flusso quasi-geostrofico.

Consideriamo un flusso zonale caratterizzato da uno shear verticale uniforme, in equilibrio con un gradiente costante di temperatura potenziale meridionale. Questo equilibrio è espresso attraverso una relazione tra la variazione della velocità del vento con l’altitudine e il gradiente di temperatura.

La configurazione del flusso viene descritta da una funzione di corrente geostrofica, che mostra che per valori positivi di altitudine, la vorticità potenziale è zero. Le isentrope, che indicano linee di temperatura costante, e la configurazione del flusso sono illustrate graficamente.

Immagina ora un’altra configurazione di flusso in cui le isentrope inclinate diventano orizzontali vicino alla superficie, in uno strato molto poco profondo. In questo strato, non ci sono gradienti di temperatura potenziale sulla superficie. La quantità media di vorticità potenziale in questo strato è stimata attraverso un’integrazione specifica attraverso lo spessore dello strato.

Con la riduzione dello spessore dello strato a un valore infinitesimale, la funzione di corrente media tende a zero, assumendo che la derivata della funzione di corrente rispetto all’altitudine sia zero alla superficie.

Questa formulazione dimostra che la presenza di un gradiente di temperatura potenziale sulla superficie è matematicamente equivalente a un flusso senza tale gradiente, ma con uno strato sottile di vorticità potenziale adiacente alla superficie. Il gradiente orizzontale di vorticità potenziale in questo strato è direttamente proporzionale al gradiente di temperatura orizzontale sopra lo strato.

Sebbene dimostrato in un caso specifico, questo è un risultato generale che collega i gradienti di temperatura orizzontali ai confini con i gradienti di vorticità potenziale.

In modo analogo, una struttura verticale dei flussi assialsimmetrici associati a isolati gradienti di temperatura superficiale mostra caratteristiche distinte per anomalie calde e fredde, rispettivamente con isentrope che si abbassano o si alzano e con circolazioni del vento cicloniche o anticioniche. Queste configurazioni sono state studiate e i risultati calcolati assumendo un particolare equilibrio dinamico.

La figura 2.1 illustra due configurazioni differenti del flusso atmosferico in un contesto quasi-geostrofico, mostrando come il gradiente di temperatura potenziale influenzi la disposizione delle isentrope e la vorticità potenziale.Figura 2.1(a):

• In questa parte della figura, le isentrope sono inclinate, estendendosi da basso verso alto con una pendenza costante. Questo rappresenta un flusso zonale con un aumento uniforme della velocità del vento con l’altitudine.
• La disposizione delle isentrope indica un cambiamento nella temperatura e nella densità dell’aria con l’altitudine, influenzando così il comportamento del flusso atmosferico in quella regione.

Figura 2.1(b):

• Qui, le isentrope diventano orizzontali in uno strato molto sottile proprio sopra la superficie, rappresentato dalla linea tratteggiata. Questo indica un’area dove i cambiamenti di temperatura vicino alla superficie sono minimi o assenti.
• Questo strato orizzontale stabilizza la colonna d’aria sopra di esso, limitando gli scambi verticali di calore. Questo strato è interpretato come un strato di vorticità potenziale, mostrando come modifiche nella disposizione delle isentrope possano indicare differenze significative nella dinamica dell’aria.

In questa spiegazione, la figura viene utilizzata per dimostrare come le modifiche nella disposizione verticale delle isentrope possono riflettere e influenzare la dinamica atmosferica, evidenziando in particolare l’effetto della temperatura sulla struttura del vento e sulla stabilità atmosferica.

2.3 Onde del Gradiente di Vorticità Potenziale

Nel primo capitolo, ho discusso come le onde di Rossby barotropiche si comportino in un canale sul piano β. Queste concetti si estendono facilmente ai movimenti ondosi quasi-geostrofici in un fluido rotante e stratificato stabilmente. Consideriamo il caso in cui esista un gradiente meridionale di vorticità potenziale di base in una certa regione. Questo gradiente è correlato al flusso zonale di base, che varia sia in direzione nord-sud che verticalmente.

A un confine orizzontale, dove si presenta un gradiente di temperatura meridionale, troviamo un contributo aggiuntivo al gradiente di vorticità potenziale in uno strato sottile al confine.

Procedendo con un’analisi semplificata, assumiamo che la vorticità potenziale perturbata abbia un’ampiezza piccola. Questo ci permette di considerare solo le variazioni di base della vorticità potenziale nel nostro studio del flusso atmosferico.

In un esempio più semplice, quando il flusso zonale varia linearmente con l’altitudine, il gradiente di vorticità potenziale assume una distribuzione uniforme in specifici strati. In alcune situazioni, queste distribuzioni nei singoli strati possono essere più significative della distribuzione complessiva associata al gradiente planetario.

Come già visto con le onde di Rossby, esistono soluzioni ondose che si propagano indipendentemente dalla direzione nord-sud e si muovono verso est, ma ora mostrano anche una struttura verticale.

Dai dati osservativi, sappiamo che i gradienti di vorticità potenziale più intensi si trovano vicino alla tropopausa e, talvolta, vicino alla superficie nelle zone barocliniche, dove i gradienti di temperatura orizzontale sono particolarmente marcati. Queste osservazioni ci portano a esaminare la propagazione delle onde lungo strati di gradiente di vorticità potenziale, specialmente in strati sottili adiacenti ai confini, conosciuti anche come fogli di vorticità potenziale. Da questo punto in poi, ci riferiremo a questi semplicemente come fogli di vorticità, poiché le teorie possono essere applicate anche a definizioni più estese di vorticità potenziale.

La figura 2.3 illustra la struttura di un’onda sinusoidale che si propaga lungo uno strato di gradiente di vorticità potenziale (PV) situato su un confine elevato. Possiamo considerare questa rappresentazione come una versione semplificata del grande gradiente di PV presente alla tropopausa. Se immaginiamo la tropopausa come un coperchio rigido situato sopra un flusso zonale uniforme, si osserverebbe un gradiente meridionale uniforme di PV in uno strato presso il coperchio, insieme a un gradiente uniforme di temperatura potenziale. Entrambi questi gradienti sono positivi. Per ora, mettiamo da parte la considerazione del gradiente di vorticità terrestre, noto come β.

Nel caso dell’onda di Rossby esaminata in precedenza, supponiamo che la perturbazione modifichi le superfici materiali, che inizialmente sono piane nei piani x-z, trasformandole in corrugazioni sinusoidali che non dipendono dall’altezza. Questo comporta delle perturbazioni di PV solo nello strato, esattamente come in un esempio precedente, ma non in altre zone. Queste perturbazioni sono collegate a variazioni della funzione di corrente che, dato che la perturbazione non varia in direzione nord-sud, assume una forma particolare.

L’uso dell’analogia con una membrana è utile ancora una volta per dedurre il modello di comportamento della funzione di corrente, che corrisponde a quello della vorticità potenziale. Iniziamo riscalandando la dimensione verticale in modo che i termini dell’equazione risultino unitari. Consideriamo quindi la funzione di corrente come lo spostamento di una membrana semi-infinita su cui viene applicata una forza sinusoidale lungo il suo bordo superiore. Dove la forza è negativa, la risposta della membrana è positiva e viceversa.

Da notare particolarmente sono due aspetti:

1. Nonostante la forza agisca al confine, la risposta della membrana si estende per una certa distanza al di sotto del confine, con una scala di penetrazione specifica.
2. Nel dominio riscalandato, il comportamento della membrana è isotropico, cioè risponde ugualmente in tutte le direzioni a una forza localizzata. Ciò implica che la scala verticale del disturbo è comparabile con quella orizzontale. Convertendo nuovamente le scale, la scala di penetrazione nello spazio fisico dipende dalla scala orizzontale considerata e viene comunemente definita come la scala di altezza di Rossby.

La perturbazione della velocità meridionale è indicata da frecce posizionate lungo l’asse orizzontale nella Figura 2.3. Si nota che questa velocità è nulla nei punti dove lo spostamento delle particelle dall’equilibrio è massimo, e raggiunge il suo picco verso ovest rispetto al punto di massimo spostamento delle particelle verso i poli. Pertanto, come già visto per le onde di Rossby in precedenza, queste onde non aumentano in ampiezza nel tempo e si muovono verso ovest rispetto alla corrente di base.

Se consideriamo la tropopausa come una superficie flessibile che divide l’aria più stabile della stratosfera da quella meno stabile della troposfera, la struttura delle perturbazioni nella stratosfera risulterà essere un’immagine speculare di quella nella troposfera, ma con una scala di profondità ridotta.

La figura 2.3b illustra una situazione simile a quella della figura 2.3a, ma con le onde che si formano su uno strato di gradiente negativo di vorticità potenziale al confine inferiore, corrispondente al gradiente di temperatura negativo in quella regione. In questo caso, le perturbazioni della vorticità potenziale sono confinate alla superficie, ma le modifiche alla funzione di corrente si estendono verso l’interno del flusso. Anche in questo caso, le onde non crescono in ampiezza, ma, dato il gradiente negativo di vorticità potenziale alla superficie, si spostano verso est rispetto alla corrente di superficie di base.

Aggiungendo un flusso uniforme a una delle configurazioni descritte sopra, si introduce una componente di trasporto nel movimento ondoso che segue la stessa velocità. Questo significa che la direzione della propagazione della fase delle onde è relativa al flusso di base al livello dello strato di vorticità potenziale.

Questi concetti base ci permettono ora di approfondire la discussione su altri tipi di ciclogenesi, inclusi i meccanismi di instabilità baroclinica, utilizzando considerazioni sulla vorticità potenziale.

La Figura 2.2 mostra gli effetti di anomalie di temperatura semplici al confine che inducono flussi circolarmente simmetrici. Le anomalie considerate sono di due tipi: calde e fredde.

• Panello (a): Questa parte della figura illustra l’effetto di un’anomalia di temperatura superficiale calda. Tale anomalia induce una circolazione ciclonica, caratterizzata da linee di flusso che si muovono in senso antiorario attorno all’anomalia. Le frecce nere indicano la direzione del movimento dell’aria, evidenziando un pattern ciclonico. L’inserzione e il tratteggio nel diagramma suggeriscono che questa anomalia di temperatura può essere vista come equivalente a un’anomalia di vorticità potenziale (PV) ciclonica.
• Panello (b): Mostra l’effetto di un’anomalia di temperatura superficiale fredda. Qui, l’anomalia provoca una circolazione anticiclonica, con linee di flusso che si muovono in senso orario. Questo movimento è anch’esso indicato dalle frecce nere, che mostrano una dinamica anticiclonica intorno all’anomalia. L’anomalia fredda è interpretata, attraverso l’inserzione e il tratteggio, come parte di un’anomalia di PV anticiclonica.

In entrambi i casi, le anomalie di temperatura influenzano significativamente la struttura dei flussi atmosferici vicini, modificando la circolazione locale dell’aria. Questi esempi illustrano come le variazioni locali nella temperatura possano avere un impatto diretto sulla vorticità potenziale e sulla circolazione atmosferica su scala più ampia.

La Figura 2.3 rappresenta la struttura delle perturbazioni ondulatorie sinusoidali legate a strati di vorticità potenziale (PV) situati ai confini orizzontali.

• Panello (a): Mostra la struttura di un’onda che si trova su uno strato di PV con un gradiente meridionale positivo al confine superiore. Le linee continue rappresentano le isosuperfici di PV, che segnalano zone di intensa attività ciclonica o anticiclonica a seconda della curvatura delle linee. Le linee tratteggiate rappresentano le superfici equipotenziali o linee di corrente costante. L’interazione tra queste due tipologie di linee dimostra come le onde si propagano e come la vorticità si distribuisce lungo l’asse zonale (y) e verticale (z). Le frecce indicano la direzione del flusso del fluido, suggerendo una dinamica complessa che varia con la profondità.
• Panello (b): Illustra la struttura corrispondente per uno strato con un gradiente negativo al confine inferiore. Qui, le linee continue che rappresentano le isosuperfici di PV mostrano una direzione del flusso opposta rispetto al pannello (a). Le linee tratteggiate continuano a rappresentare le superfici equipotenziali.

In entrambi i pannelli, l’effetto del gradiente di PV è evidente nella forma e nella direzione delle onde e delle correnti. Questi diagrammi sono utili per comprendere come le variazioni localizzate di vorticità potenziale influenzino la struttura del flusso atmosferico su larga scala, evidenziando comportamenti diversi a seconda del segno del gradiente di PV e della sua posizione rispetto ai confini orizzontali.

2.4 Instabilità Baroclina

Per approfondire i meccanismi di formazione dei cicloni, è utile esaminare il problema dell’instabilità baroclina, che considera l’evoluzione di disturbi iniziali in una corrente baroclina. Uno degli esempi più semplici è quello studiato da Eady nel 1949, che ha analizzato la stabilità di un flusso zonale uniforme con uno scorrimento verticale della velocità, rispetto alle perturbazioni ondulatorie quasi-geostrofiche. In questo modello, non si considera la variazione del parametro di Coriolis, presumendo che sia costante, e si assume che il flusso sia limitato tra due confini orizzontali.

All’interno del flusso, il gradiente meridionale del vortice potenziale (PV) è nullo, ma ai confini si formano strati di PV con un gradiente negativo al confine inferiore e positivo al confine superiore. Questo permette di immaginare i disturbi come composti da onde di gradiente di vorticità potenziale. In particolare, le onde instabili nel modello di Eady possono essere interpretate come due onde sinusoidali della stessa lunghezza d’onda, una associata al gradiente di PV al confine superiore, l’altra al confine inferiore.

Un risultato ben noto indica che queste onde instabili si muovono alla velocità del flusso nella parte centrale del canale, definita come il livello di guida per queste onde. Questo principio di guida è spesso utilizzato come regola pratica nelle previsioni meteorologiche, indicando che le perturbazioni atmosferiche profonde tendono a muoversi con il flusso a circa 500 mb di altitudine. In relazione a questo flusso di guida, l’onda superiore si muove verso ovest ma è spinta verso est dalla corrente, mentre l’onda inferiore si muove verso est ma è spinta verso ovest. La velocità e la direzione effettive di ciascuna onda dipendono dalla loro lunghezza d’onda; se la lunghezza d’onda è sufficientemente lunga, la propagazione predomina sull’advezione, altrimenti è l’advezione a prevalere. Esiste tuttavia una lunghezza d’onda specifica alla quale le onde risultano stazionarie rispetto al sistema di riferimento che si muove con la velocità di guida.

Immagina una situazione in cui le due onde sono sfasate; per esempio, considera che l’onda associata al confine superiore sia posizionata a ovest rispetto a quella del confine inferiore.

Quando i disturbi generati da ciascuna delle due onde si sovrappongono, ossia quando la distanza D è maggiore o uguale all’altezza H, si verifica che la perturbazione della velocità meridionale dell’onda superiore è positiva laddove l’onda inferiore raggiunge il suo massimo spostamento meridionale, e viceversa. Questo implica che ogni onda contribuisce ad accrescere gli spostamenti meridionali e, di conseguenza, l’ampiezza dell’altra onda. In questa configurazione di fase, le due onde tendono a crescere insieme nel tempo. Questa configurazione di fase corrisponde a quella che, basandosi sull’esperienza di previsione meteorologica, si ritiene favorisca una continua ciclogenesi nell’atmosfera, confermando una delle previsioni della teoria di Sutcliffe.

Se, al contrario, la fase è invertita, cioè se il minimo superiore si trova a est rispetto a quello inferiore, la perturbazione della velocità meridionale dell’onda superiore risulta negativa nel punto in cui l’onda inferiore mostra il massimo spostamento meridionale. In questo scenario, le onde contribuiscono reciprocamente al loro decadimento, seguendo la struttura dei modi di decadimento nel problema di Eady.

Quando le onde superiore e inferiore sono in fase, ossia quando il minimo superiore si allinea esattamente sopra quello di superficie, la perturbazione della velocità meridionale di ciascuna onda si annulla nei punti di massimo e minimo spostamento meridionale dell’altra, e come per le onde di Rossby, non si osserva crescita. Questa è la struttura delle soluzioni stabili neutre nel problema di Eady. Questa situazione riflette anche un’osservazione comune nella previsione meteorologica: quando il minimo di superficie si trova direttamente sotto la trincea superiore, non si prevede un ulteriore approfondimento del sistema. Anche questo è un risultato corroborato dalla teoria di Sutcliffe.

Per capire come due onde possano finire in una specifica configurazione di fase, è necessario analizzare il problema del valore iniziale, studiando come un disturbo iniziale qualsiasi possa essere scomposto nei modi sinusoidali elementari di cui abbiamo discusso. Purtroppo, il tempo a disposizione non mi consente di approfondire questa tematica né di esplorare le ragioni per cui due onde, una volta allineate in fase, tendano a rimanere sincronizzate nella loro crescita. Per ulteriori dettagli, rimando al lavoro di McIntyre (1985b, §9). Tuttavia, abbiamo posto le basi per comprendere altri meccanismi di ciclogenesi oltre a quello descritto nel primo capitolo.

La figura 2.4 illustra il comportamento della corrente guida e del flusso relativo in un flusso di taglio zonale uniforme, evidenziando come le onde di vorticità potenziale (PV) si muovano ai confini del flusso.

1. Corrente Guida (steering current): La linea diagonale continua rappresenta la corrente guida, che si inclina verso destra (est) con l’aumentare dell’altezza (z). Questo mostra la direzione prevalente del flusso atmosferico medio in questo modello, che varia linearmente con l’altezza.
2. Flusso di Taglio Zonale (U(z)): La linea diagonale tratteggiata indica il flusso di taglio zonale, che segue la stessa inclinazione della corrente guida, mostrando la variazione lineare della velocità con l’altitudine.
3. Onde di Gradiente di Vorticità Potenziale (PV): Le frecce ricce rappresentano le onde di PV che si propagano ai confini del sistema:
   • Onda superiore (C upper wave): Propagata verso sinistra (ovest), come mostrato dalla freccia riccia in alto.
   • Onda inferiore (C lower wave): Propagata verso destra (est), come mostrato dalla freccia riccia in basso.
4. Advezione Relativa: Le frecce indicano la direzione dell’advezione relativa delle onde rispetto alla corrente guida. Nonostante l’onda superiore si muova verso sinistra, essa viene trascinata verso destra dalla corrente guida. Inversamente, l’onda inferiore, che si propaga verso destra, è influenzata dalla corrente guida che la spinge verso sinistra.

Questi elementi dimostrano come l’interazione tra le onde di PV e la corrente guida determini il movimento delle perturbazioni atmosferiche, fornendo una chiave di lettura essenziale per comprendere la dinamica dei cicloni e altre perturbazioni meteorologiche.

2.5 Applicazioni alla comprensione della ciclogenesi

Alla conclusione del capitolo 1, ho delineato un meccanismo molto basilare per la ciclogenesi che non coinvolge il processo di instabilità baroclinica. Tale instabilità, come precedentemente descritta, potrebbe essere responsabile dello sviluppo di alcuni cicloni a partire da disturbi incipienti in un flusso baroclinico di taglio, ma ciò è difficile da verificare non avendo la possibilità di osservare direttamente il disturbo incipiente. Nella maggior parte dei casi, sembra che la ciclogenesi avvenga alla presenza di perturbazioni di ampiezza finita. Tuttavia, i concetti appena descritti possono essere applicati anche a questi scenari più realistici.

Basandosi su risultati che risalgono a Sutcliffe (1947), i sinottici si focalizzano sulla presenza di una “onda corta” o di una “gola d’onda corta” nelle mappe della alta atmosfera. In termini di vorticità potenziale (PV), queste sono collegate a anomalie cicloniche di PV, generalmente intorno al livello della tropopausa, come illustrato nelle Fig. 1.6 e 1.7. Si presume che abbiano una struttura verticale analoga a quella presentata nelle Fig. 1.10-1.11.

HMR esaminano cosa succede quando un’anomalia di PV dell’alta atmosfera viene trasportata sopra una regione baroclinica di basso livello, come mostrato nella Fig. 2.5.

Si ipotizza che in (a) l’anomalia, rappresentata da un segno più solido e associata a una tropopausa bassa, sia appena arrivata sopra una regione di marcata baroclinità a basso livello. La circolazione indotta dall’anomalia è rappresentata da frecce solide, e i contorni di temperatura potenziale sono visibili al suolo. La circolazione a basso livello è rappresentata sopra il terreno per maggiore chiarezza.

L’advezione generata da questa circolazione produce un’anomalia di temperatura calda a est dell’anomalia di PV superiore come mostrato in (b), evidenziata da un segno più vuoto. Questa anomalia calda provoca la circolazione ciclonica indicata dalle frecce vuote in (b). Se il movimento verso l’equatore ai livelli superiori trasporta aria di alta PV della bassa stratosfera polare, e il movimento verso i poli trasporta aria di bassa PV della alta troposfera subtropicale, l’azione della circolazione di alto livello indotta dall’anomalia di PV superficiale, in effetti, rafforza l’anomalia di PV dell’alta atmosfera. Questo rallenterà anche la sua propagazione verso est, come discusso da McIntyre (1988b).

(i) Il grado di ciclogenesi dipenderà da numerosi fattori. (ii) La forza dell’anomalia di PV dell’aria superiore. (iii) La scala di profondità di Rossby, D = fL/N, in relazione all’altitudine di questa anomalia rispetto alla superficie. Qui, H rappresenta la scala di lunghezza orizzontale dell’anomalia. (iv) La forza dell’anomalia a basso livello, che dipenderà, tra l’altro, dalla quantità di advezione calda a basso livello, e (v) La misura in cui il blocco di fase e l’amplificazione reciproca delle anomalie di superficie e dell’aria superiore sono significativi.

Gli ultimi tre fattori sono profondamente influenzati dal rilascio di calore latente che, tra l’altro, influisce sulla stabilità statica N e quindi sulla penetrazione verticale delle due separate anomalie di PV.

In relazione al punto (iv), potrebbe non essere il caso che le perturbazioni superiori e inferiori rimangano in fase abbastanza a lungo perché lo sviluppo corrisponda strettamente al meccanismo dell’onda baroclinica descritto in precedenza. Tuttavia, anche un’interazione temporanea delle due perturbazioni può portare a un grado di ciclogenesi di notevole interesse per il previsionista.

Nell’esempio descritto sopra, si supponeva che entrambe le anomalie superiori e inferiori fossero immerse in un ambiente con un ampio gradiente di PV su larga scala. Se ciò non accade, il meccanismo di instabilità baroclinica non può operare. Tuttavia, quando un’anomalia passa sopra l’altra, ci sarà un rinforzo temporaneo di ciascuna durante il periodo in cui sono in fase e questo potrebbe anche portare a un evento ciclogenetico di significato per il previsionista.

Alcune interessanti rappresentazioni tridimensionali dell’interazione tra anomalie di PV superiore e inferiore associate alla ciclogenesi extratropicale sono contenute in un articolo di Bleck (1990).

La Figura 2.5 illustra un modello schematico della ciclogenesi risultante dall’arrivo di un’anomalia di vorticità potenziale (PV) nell’alta atmosfera sopra una zona baroclinica a basso livello.

• Panello (a): Presenta l’inizio del fenomeno con l’arrivo dell’anomalia di PV superiore, contrassegnata da un segno più (+), al di sopra della zona baroclinica, distintamente rappresentata con aree colorate per indicare una regione calda e una fredda. Le frecce nere mostrano la circolazione indotta dall’anomalia di PV, che interagisce con il gradiente termico, generando movimenti verticali e orizzontali nell’atmosfera.
• Panello (b): Descrive l’evoluzione successiva dell’interazione tra l’anomalia di PV e la zona baroclinica. L’anomalia di PV, ancora indicata dal segno più (+), genera una circolazione più elaborata come illustrato dalle frecce nere che si muovono in diverse direzioni. Questo complesso schema di circolazione accentua i contrasti termici, culminando nella formazione di una nuova anomalia di temperatura calda a est dell’anomalia di PV, visibile dalle linee di temperatura potenziale che si incurvano verso l’alto. Questo riscaldamento può rafforzare ulteriormente la circolazione ciclonica, favorendo la ciclogenesi.

In conclusione, la figura dimostra come l’interazione dinamica tra un’anomalia di PV superiore e una zona baroclinica di basso livello possa innescare e intensificare un ciclone, evidenziando l’importanza dei movimenti verticali e orizzontali, nonché dei cambiamenti nelle proprietà termiche dell’aria, nel processo di ciclogenesi.

Capitolo 3: Invertibilità, grafici iso-PV, effetti diabatici e frizionali

3.1 Invertibilità dell’EPV

Nell’ultima lezione, abbiamo esteso le idee della dinamica quasi-geostrofica ai cicloni reali, dove l’approssimazione quasi-geostrofica può risultare imprecisa. Nelle applicazioni atmosferiche, preferiamo utilizzare l’EPV piuttosto che il PV, dato che l’EPV è conservato in condizioni più ampie. Tuttavia, a differenza del PPV, non è possibile invertire l’EPV per analizzare il flusso legato alle anomalie di EPV senza assumere un certo equilibrio. L’equilibrio geostrofico può non essere abbastanza preciso per analisi quantitative, ma esistono altre opzioni. Non è il caso di approfondire qui; per una discussione dettagliata si rimanda a HMR e a Davis (1992), e per un esempio pratico a Davis ed Emanuel (1991). Per ottenere spunti qualitativi, si può avanzare molto supponendo un equilibrio quasi-geostrofico.

3.2 Grafici iso-PV

Nella prima lezione, abbiamo osservato che durante un movimento adiabatico e senza attrito, una particolare proprietà P è conservata mentre si segue una particella d’aria. Analogamente, anche θ è conservato, il che significa che entrambe le proprietà sono mantenute su specifiche superfici all’interno dell’atmosfera. In particolare, questa conservazione si verifica vicino alla tropopausa nelle latitudini extra-tropicali, un’area dove i gradienti di questa proprietà sono particolarmente marcati e quindi di grande interesse per l’analisi delle anomalie a livelli superiori. In questo contesto, è emerso che i gradienti orizzontali di questa proprietà sono simili ai gradienti di temperatura orizzontali. Per questo motivo, invece di utilizzare molti grafici diversi su superfici isentropiche, potrebbe essere sufficiente un unico grafico selezionato. Questi grafici non solo mostrano caratteristiche simili ai più complessi grafici di questa proprietà, ma offrono anche il vantaggio di fornire indicazioni sull’altezza della tropopausa, definendo così la sua “topografia”. Tali grafici possono essere utili anche in combinazione con grafici che mostrano variazioni di temperatura a bassi livelli, come ad esempio a 850 mb. Un esempio di questo approccio è stato presentato da Hoskins e Berrisford nel 1988.

3.3 Effetti Diabatici e Frizionali

Quando sono presenti effetti diabatici e/o frizionali, il PV non rimane costante materialmente ma è influenzato da questi fattori. Il PV è modificato dalla vorticità assoluta e dal riscaldamento diabatico, così come dalla forza frizionale per unità di massa. Ad esempio, il riscaldamento diabatico in una regione localizzata può creare una anomalia dipolare nel PV, orientata in base alla direzione della vorticità.

L’integrazione di questi effetti su un’area specifica mostra che i cambiamenti interni dovuti al riscaldamento o alla frizione non alterano la distribuzione complessiva del PV all’interno dell’area, a meno che questi processi non siano presenti sulla superficie dell’area considerata.

Inoltre, l’applicazione di una forza localizzata può alterare la vorticità relativa creando vorticità positiva da un lato e negativa dall’altro. Questo contribuisce a modificare ulteriormente il PV nella regione interessata. Nel caso di un vortice assisimmetrico, una forza frizionale che agisce a livello del suolo può degradare il PV localmente. Questo tipo di interazione è particolarmente significativo nei pressi dello strato limite atmosferico.

Questa interpretazione suggerisce che le modifiche apportate al PV attraverso questi meccanismi non si traducono in un trasporto attraverso le superfici isentropiche, anche se gli effetti diabatici sono presenti. Questo è un risultato chiave per comprendere il comportamento del PV in condizioni meteorologiche complesse.

La Figura 3.1 rappresenta diverse situazioni in cui sono coinvolti cambiamenti nel potenziale vortico (PV) causati da riscaldamento diabatico localizzato, raffreddamento, e l’azione di una forza localizzata.(a) Riscaldamento diabatico localizzato: Questo diagramma illustra come il riscaldamento in un’area specifica possa creare cambiamenti nella distribuzione del potenziale vortico (PV). Il riscaldamento induce una variazione del PV lungo una direzione specifica, generando un modello a dipolo, dove un lato mostra un aumento e l’altro una diminuzione.

(b) Raffreddamento diabatico localizzato: Al contrario del riscaldamento, il raffreddamento inverte l’orientamento del dipolo di PV. In questo caso, la parte che precedentemente mostrava un aumento a seguito del riscaldamento ora mostra una diminuzione, e viceversa.

(c) Forza localizzata FFF: Questo pannello mostra l’effetto di una forza applicata in un punto specifico e come essa influenzi la vorticità. La forza genera vorticità relativa positiva da un lato e negativa dall’altro, formando così un dipolo di vorticità. Questo effetto è essenziale per comprendere come le forze esterne modifichino il movimento dell’aria nell’atmosfera.

Ogni parte di questa figura dimostra l’importanza di comprendere come variazioni specifiche, sia termiche che meccaniche, possano impattare significativamente la dinamica atmosferica.

Effetti del riscaldamento diabatico sulla ciclogenesi

I processi legati all’umidità possono migliorare notevolmente lo sviluppo in superficie diminuendo la stabilità statica effettiva. Questo incremento nella profondità a cui possono estendersi le perturbazioni porta a un maggiore contatto dinamico tra le anomalie di potenziale vorticoso ai livelli alti e bassi dell’atmosfera, risultando in uno sviluppo più marcato. Questa intensa interazione contribuisce anche a rallentare il movimento relativo dell’anomalia superiore rispetto a quella inferiore, aumentando il livello di sincronizzazione tra di esse. Inoltre, il rilascio di calore latente nella media troposfera tende a diminuire l’anomalia del potenziale vorticoso, come mostrato in un’illustrazione precedente.

Declino dei Cicloni Tagliati e degli Anticicloni di Blocco

Considera un ciclone tagliato associato ad un’anomalia di potenziale vorticoso (PV) a livello alto, come discusso nella Lezione 1 (vedi Fig. 2.4 e 2.5). Gli autori HMR notano che l’area sotto l’anomalia, caratterizzata da una stabilità statica ridotta (vedi Fig. 1.10a e 1.11), è propensa alla formazione di convezione profonda. Il rilascio di calore latente in queste condizioni può generare un’anomalia di PV a doppio polo, con una componente negativa in alto che tende a indebolire l’anomalia superiore, e una positiva in basso che la rafforza ai livelli inferiori. In pratica, la convezione sposta verso il basso l’anomalia di PV ciclonico. Secondo HMR, per eliminare completamente il ciclone, la ridistribuzione verticale di PV indotta diabaticamente dovrebbe estendersi fino alla superficie e dovrebbe avvenire insieme alla distruzione del PV integrato in massa a causa dell’attrito superficiale, come discusso nella sezione 3.3. Essi dimostrano che il rilascio di calore latente durante convezioni troposferiche profonde può portare a un decadimento diabatico efficiente di un’anomalia di PV superiore nel giro di pochi giorni.

Un aspetto unificante del “pensiero PV” è la dualità concettuale che esso offre tra i cicloni tagliati e gli anticicloni bloccanti. Questi ultimi sono legati ad anomalie anticicloniche di PV nelle altezze e sono caratterizzati da una tropopausa elevata con isentropi abbassate sotto l’anomalia, il che indica una maggiore stabilità statica in quella zona. Tuttavia, la modifica diabatica di queste formazioni tende a essere molto più rapida nei cicloni rispetto agli anticicloni. HMR evidenziano che la principale differenza sta nella stabilità statica troposferica indotta dall’anomalia di PV, che sopprime la convezione profonda e lascia il raffreddamento radiativo come il principale processo diabatico, portando a un tempo di decadimento di circa una settimana.

Vantaggio dell’Analisi PV nei Cicloni Tagliati

I meteorologi hanno tradizionalmente distinto i sistemi meteorologici “tagliati” da quelli “non tagliati” attraverso la presenza o assenza di contorni geopotenziali chiusi nei livelli medio e alto della troposfera. Secondo HMR, questa distinzione è inadeguata perché non è invariante rispetto a trasformazioni galileiane; ovvero, aggiungendo una velocità di traslazione uniforme all’intero sistema, la sua classificazione potrebbe cambiare nonostante la dinamica rimanga inalterata. Al contrario, la struttura del potenziale vorticoso (PV) è invariante galileiana e offre quindi una base più solida per distinguere tra sistemi con e senza taglio.

Definizione di Cicloni Tagliati

I cicloni tagliati, noti anche come “cut-off lows”, sono aree di bassa pressione atmosferica che si sono separate o “tagliate” dal flusso principale della corrente a getto. Questi sistemi possono formarsi sia a livelli medi che alti della troposfera. Una volta tagliati dalla corrente a getto, i cicloni tagliati possono diventare quasi stazionari, portando a condizioni meteorologiche persistenti nella regione influenzata. Tali condizioni includono spesso precipitazioni prolungate, nuvolosità e, a seconda della stagione e della località, possono anche includere fenomeni come neve o temporali. La loro evoluzione è indipendente dalla dinamica del flusso atmosferico principale, rendendoli fenomeni significativi e talvolta problematici da prevedere.

Struttura PV dei Cicloni Tropicali

Un aspetto cruciale della ciclogenesi tropicale è il rilascio di calore latente durante intensi fenomeni di convezione profonda. Questo processo di riscaldamento generalmente induce la formazione di un’anomalia ciclonica di potenziale vorticoso (PV) ai livelli bassi e un’anomalia anticiclonica nella parte superiore della troposfera (vedi Fig. 3.1a). In un ciclone tropicale, questa distribuzione viene trasportata dalla circolazione meridionale, estendendo l’anomalia a basso livello attraverso la maggior parte della troposfera e diffondendo l’anomalia anticiclonica in uno strato ampio, ma superficiale, proprio sotto la tropopausa. Il modo in cui queste strutture si sviluppano è stato illustrato tramite un modello semplificato di calcolo da Schubert e Alworth nel 1987. La figura 3.2 presenta i risultati di un calcolo simile effettuato da Möller e Smith nel 1994, in cui un vortice viene generato attivando una fonte di calore fissa in una zona anulare attorno all’asse di rotazione, configurazione che mira a simulare in modo approssimativo l’effetto del rilascio di calore latente nelle nuvole che formano la parete dell’occhio di un ciclone tropicale.

La figura 3.2 mostra l’evoluzione della struttura del potenziale vorticoso (PV) e della velocità del vento tangenziale in un modello di ciclone tropicale, utilizzando un approccio calcolato da Schubert e Alworth nel 1987. Il diagramma illustra come una fonte di calore simmetrica e fissa, posizionata intorno all’asse di un fluido che ruota uniformemente, influenzi la dinamica del sistema. La fonte di calore viene introdotta all’inizio del modello e i pannelli visualizzano le variazioni nei campi a intervalli di 24 ore.

Dettagli della Figura 3.2:

• Diagrammi superiori: Questi rappresentano le isolinee del PV adimensionale. Il PV è cruciale per comprendere la rotazione e la dinamica dei fluidi in un ciclone. Le modifiche al PV causate dalla fonte di calore sono chiaramente visibili, evidenziando come il sistema si evolve nel tempo.
• Diagrammi inferiori: Mostrano la velocità del vento tangenziale, che circola attorno al centro della perturbazione. Questo parametro è fondamentale per analizzare la forza e la struttura del vento che influenzano direttamente la formazione e l’evoluzione del ciclone.
• Coordinate usate nei diagrammi: Le coordinate verticali sono isentropiche, basate su superfici di uguale entropia, mentre le coordinate orizzontali sono radiali stiracchiate per mettere in risalto specifiche dinamiche del flusso.

Importanza della Figura:

Questa rappresentazione è essenziale per comprendere come la fonte di calore influenzi la struttura del ciclone, alterando il PV e la dinamica dei venti. In un contesto reale, tali fonti di calore possono essere rappresentate da intensa convezione all’interno delle pareti dell’occhio di un ciclone tropicale, giocando un ruolo chiave nella dinamica del sistema.

In conclusione, la figura 3.2 offre una visione dettagliata e quantitativa di come un ciclone tropicale possa evolversi sotto l’effetto di una fonte di calore persistente, dimostrando cambiamenti significativi nel potenziale vorticoso e nella velocità del vento nei dintorni del centro del ciclone.

https://www.meteo.physik.uni-muenchen.de/lehre/roger/Adm_Lectures/PV.pdf